Isaac Newton revolucionó el campo de la física, cuando en 1687 publica “Philosophiae naturalis principia mathematica”, también conocidos como “Principia”.
En esta publicación, Newton estableció los fundamentos de la mecánica clásica a través de sus leyes, encontradas y comprobadas a través de experimentación.
En este artículo te explicaremos uno de los conceptos a los que Newton dio pie y que a día de hoy sigue siendo un tanto misterioso: “G”, o la constante gravitatoria universal.
¿Qué es la gravedad?
A todos nos suena la famosísima historia según la cual Isaac Newton se da cuenta de la existencia de la gravedad tras un accidente bajo un manzano, en el que le cayó una manzana en la cabeza. Según el propio Newton, este fenómeno le reveló que una fuerza estaba tirando de la manzana hacia la tierra, cosa que acabaría demostrando al postular sus cálculos para la gravedad en sus Principia.
La gravedad es una fuerza fundamental del universo, según la cual todo aquello que posea masa ejerce una atracción sobre el resto de objetos. Esta atracción ocurre entre los planetas y las estrellas, las tostadas y el suelo, o cualquier sistema que se te pueda pasar por la mente, siempre que tengan masa.
Isaac Newton definió la ecuación que permitía calcular la fuerza gravitatoria entre dos objetos como las masas de los objetos atrayentes dividida entre la distancia entre ellos al cuadrado, multiplicado por una constante a la que nombró "G".
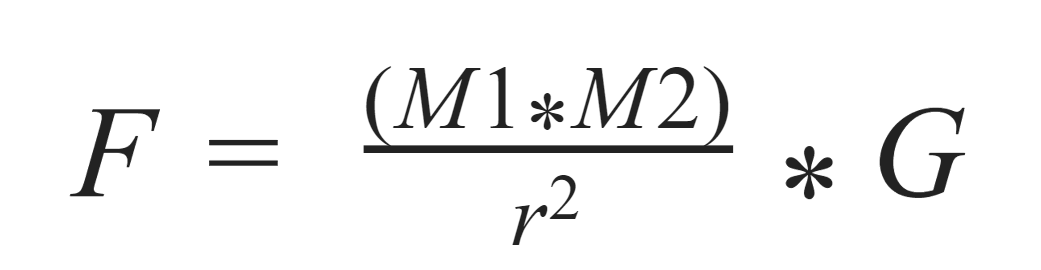
Cuando hablamos de objetos de tamaño similar, se utiliza esta ecuación. Pero la fuerza gravitatoria terrestre en su superficie es conocida, un valor de aceleración de 9.8 m/s sobre todos los objetos que se encuentran sobre ella. Cuando hablamos de masas tan dispares como las de un planeta sobre un ser humano o una manzana, las masas de estos últimos son prácticamente negligibles debido a su pequeñez.
De ahí que pese a tener masas distintas y además, que la ecuación gravitatoria dependa de la masa de ambos objetos, la fuerza de la gravedad terrestre se mantiene relativamente similar independientemente del objeto que estemos comprobando.
- ¿Te interesa la ciencia? "Las diferencias entre cáncer y carcinoma"
¿Qué es G?
G tenía un valor que Newton desconocía, ya que no conocía tampoco la masa del planeta tierra. Se denominó constante gravitatoria universal y Newton sabía que tenía que ser de un valor increíblemente pequeño, ya que los efectos gravitatorios entre objetos cotidianos no se observan en el día a día.
Newton tenía razón respecto a las características de G, pero no fue hasta 1798 cuando el increíble filósofo natural (revolucionario químico y físico de la época) Henry Cavendish calculó experimentalmente el valor de G, utilizando un modelo experimental de otro increíble físico de la época amigo suyo, John Mitchell.
Como curiosidad podríamos mencionar que John Mitchell también fue un avanzado a su tiempo, postulando la posible existencia de agujeros negros, un método de manufacturación de imanes artificiales o que los terremotos viajaban en ondas. Los únicos detalles conocidos del físico de Mitchell son que era un hombre bajito, gordo y de complexión negra.
Tras la muerte de John Mitchell, Henry Cavendish continuó uno de los experimentos que le legó. Una manera de medir la fuerza gravitatoria entre dos objetos, mediante un sistema de elementos aislados en suspensión. De esta forma Henry Cavendish consiguió calcular la constante gravitatoria universal, G.
- Quizás te interesa: "Los 8 tipos de enlaces químicos entre átomos y moléculas"
¿Cuanto vale G?
Actualmente el valor de G se acepta como 6.66704810 x 10^-11, un valor increíblemente pequeño que cuadra con las estimaciones de Newton. Los experimentos de Cavendish consiguieron acercarse a este valor, con una estimación un 1% errónea respecto a nuestros conocimientos actuales.
El valor de G es motivo de disputa incluso aún en día, a pesar de utilizarse en ecuaciones físicas muy importantes. Esto se debe a una varios motivos, tales como:
1. La gravedad afecta a todos los objetos con masa
Es complicado medir la gravedad ya que los aparatos de medición que utilicemos tendrán masa y ejercerán un efecto sobre el experimento. La cantidad de factores a considerar para calcular de forma exacta la fuerza de atracción entre objetos reales es muy intimidante, ya que cualquier objeto puede ejercer influencia sobre el sistema que estamos midiendo.
2. No podemos derivar G a partir de otras constantes
Existen muchas constantes y valores que se utilizan en ciencia que son inferidos en lugar de medidos. Por desgracia este no es el caso con la constante de gravitación universal, que a día de hoy necesita medirse experimentalmente
Actualmente a pesar de que utilizamos un valor concreto de G, sabemos que este valor no es necesariamente el correcto, si no la mejor estimación que hemos podido sacar de un rango de valores que es demasiado amplio.
¿Es útil la constante de gravitación universal?
Por supuesto. La constante de gravitación universal es un valor que podemos utilizar en múltiples fórmulas con diferentes aplicaciones. Gracias a nuestras estimaciones de G, podemos conocer la fuerza gravitatoria que ejercen los planetas sobre los objetos de su superficie.
Además, la constante gravitatoria universal aparece en las ecuaciones de Max Plank en las cuales determinó la distancia más corta posible en el universo (la distancia de Plank) así como el intervalo temporal más corto posible (el tiempo de Plank).
La ciencia no debería actuar de forma dogmática, como si todo lo que se ha dicho en el pasado fuera cierto. Personas como Newton, capaces de cambiar nuestros paradigmas, nos recuerdan que nos hemos de mantener humildes acerca de las explicaciones que le damos al universo, ya que pueden existir factores ignorados que nos lleven a otras conclusiones.
La constante gravitatoria universal no es una excepción. Con valores constantemente revisados para poder definirla de manera cada vez más precisa, se utiliza constantemente a pesar de que no sabemos el por qué de su valor ni su valor exacto.
Lo más importante en estos caso es reconocer que no tenemos toda la información, pero podemos seguir avanzando sabiendo que existen agujeros en nuestro conocimiento. Si estos agujeros tienen importancia o no, lo sabremos una vez queden esclarecidos.
















